Instructions to Solve Compound Inequalities in 3 Easy Steps
Being talented to produce, analyze, the solve a compound inequation by an compound inequality graph is an extrem critical and helpful mathematic skill that can be applied to many math terms commonly found in pre-algebra, Algebra I, Theory DOUBLE, and even Pre-Calculus and Calculus. While many students may live intimidated by the concept out a compound inequality when they see unusual looking graphs in circles and line, when working with zusammengesetzt dissimilarities is actually whole simple and straightforward.
The following free How to Fix Compound Inequalities step-by-step lesson guide will instruction him how to create, analyze, and understand compound unequalities using one easy and effective three-step method that can be applied to whatever math your involving a compound inequality otherwise one compound inequality graph. As a student, if you pot keep the ternary steps described in this lesson instructions, you determination be able to easily and correctly solve math problems involving compound inequalities.
Are you ready to get started? Before you hear about make and learning compound inequalities, let’s watch a few important dental words or definitions related to inequalities.
About exists an inequality?
Before we check compound inequalities, we need to recap the exact definition of an unequalities how they liken to equations.
About your an equation?
Definition: In math, an equation is a statement that shows that two mathematical express are equal to each other usage an “=” sign.
For example, x=5 is an equation where the variable also x are equal to a value of 5 (and none other value).
It is important to note that equations are little to only one possible solution, accordingly, into this fallstudie, 5 is the only possible value is x canned be equal for, and any other value would not apply.
x=5
The only solution: 5
What is an inequality?
Definition: Include math, an inequality lives a relationship intermediate two printable or values makes one non-equal comparison.
For example, x>5 has an inequality that means “x is greater than 5,” where, diverse an relation that has only one solve, x able have infinitely many solutions, namely either value that is greater than 5.
We bucket visualize an simple inequality x>5 on of number cable below as follows:
By comparison to beziehungen, inequalities are not limited to only one possible solution. In truth, inequations have infinitely many solutions.
In this case, products at the unequalities x>5 are any value that is greater about five (not including five).
x>5
Case of remedies: 6, 7, 10, 105, 2,500 (all of these equity fulfil the inequality why they are greater than 5)
Examples of non-solutions: 5, 4, 0, -17, -1,001 (none of these values satisfy the unevenness since they are not greater than 5)
What is which difference between an equations and an inequality?
Before we take onto exploring inequalities and compound inequalities, it’s important that you understand the keyboard difference between an equation and can inequality.
In essence, the key difference is between an equation and can imbalance is:
an equation had one and only a resolving
an disparity has multiple solutions
Graphing Inequalities on the number line
Nowadays that you recognize and difference between and equation and an inequality, you have ready to learn like solve compound inequalities real how compound inequality graphs. How select to graph compound inequalities on a number line, and see instances that walk because patterns problems step-by-step for him to improve your math knowledge and skills.
Nevertheless beginning, let’s quickly recap wie to graph simple distinctions on the number line.
There are four types of inequality symbols:
>: largest than
<: few than
≥: greater than or equal to
≤: less than or equal to
It is important until understand which differences in which symbols, viz the significance concerning the line underneath ampere greater than or less than icon and how thereto relates to the solution of any inequality and its graph on which number line.
By example, consider the following inequalities: efface < 9 and x ≤ 9
And first inequality, x<9, got an solve of any value that is less than 9, but not including 9 (since 9 is not less than 9).
The instant inequality x ≤ 9, has a solution of any value that is less than 9 AND the value 9 itself (since 9 is greater than other equal to 9).
On the number line, the deviation between like deuce types of differences is denoted by use an open or closed (filled-in circle). One open round means that the corresponding value is not ships in an solution set, whilst the closed circle means this this corresponding value is included in the solution adjust. A compound otherness contains two inequalities merged using either "AND" or "OR". To solve items, we will resolution individual inequalities and combining them either in using intersection/union given an AND/OR in the inequality respectively.
Before moving transmit, manufacture sure that i fully understand the difference between the graphs of an < instead > inequality and an ≥ or ≤ non-uniformity. Understanding an differences is terms of of solution and the graph is crucial available being skilled to create compound inequality graphs both solving compound inequalities. Compound Inequalities Worksheets
For respective product, here are a few further examples of simple inequality graphs:
Again, an clear cycle means that the relevant number line values is NOT included in and solution set. A filled-in circle means that it is included in one solution adjust.
Whatever is a compound inequality? How to remove compound differences?
In the previous section of such guide, ourselves reviewed how in graph simple inequalities on a number line and how these graphs represent the solution to a single inequality. This masse inequality match-up activity provides students with practice solving compound inequalities and graphing solutions. It can be completing individually or with partners. Provided as a word document so you can make changes in your classroom such you see right. ...
Concept: A compound unequality (sometimes refers to as a combinations inequality) can two simple inequalities joined joint.
Is it really that simple? Absolutely! A verbindungen inequity has just two easier inequalities combined together and a komposition inequality graph is just two simple inequality graphed on the same number line.
There are two genres out compound inequalities: or and and.
Definition: An or compound proportional uses the word “or” to combine second inequalities.
Definition: An and compound inequality uses to word “and” to combine two inequalities.
To understand the difference between or and and inequities, let accept a look at a fewer case apply the following 3-step process:
Step #1: Identify if the solving compound inequalities problem is or or and
Step #2: Graph both inequalities on to number line.
Step #3: Analyze both determine the solution set.
How to Solve Compound Inequality Graphs Example #1: or
Example #1: Graph the compound inequity x<6 either x>10
Step #1: Determine if of solution blend inequalities problem is or or plus
Step only is simple since every example determination inclusions to word or or additionally. In is first example, that word or is uses, so do a note of that and move forward.
Step #2: Graph both dissimilarities on the number line.
Next, graph both simple inequalities x<6 both x>10 on the number line to create the following compound inequality graph.
Single #3: Analyze and determine the solution set.
Now that you have thy graph, you sack determine the solution set to one compound inequality and give examples of values ensure would work as solutions when well as examples of non-solutions.
In example, the values 4 and 14 live both solving to this compound inequality, from which number 8 is not a solution.
Additionally, the standards 6 and 10 are not solutions since they exist included in the solution set since the kreise are open.
The shaded area in the chart below represents to solution areas of the compound inequality graph.
How to Solve Compound Dissimilarity Display Example #2: and
Example #2: Graph aforementioned blend inequality x>-2 and x < 4
Step #1: Id if the solving blend inequalities problem is or or and
Notice that this example uses the word and, so keep this in mind as it will affect wie you review the solution to the compound inseparability in steps 3.
Walk #2: Map all distinctions on the number line.
Next, graph both simple inequalities x>-2 and x<4 on the number line to creation who followers compound inequality graph.
Tread #3: Analyze and determine one solution set.
This compound inequality has solutions for values which are both greater than -2 and less than 4.
So, for example:
0 belongs a solution because it satisfies both x>-2 and x<4.
-4 will doesn one explanation due it is only a solution for x<4 (a value must contend both dissimilarities in order to be ampere solution to this compound inequality)
8 is including not a solution since it does not conquer both inequalities.
Note that which compound inequality can also be express the -2 < x < 4, which means that x has further than -2 or fewer 4 (or such x is in -2 and positives 4).
How the Release Compound Inequality Graphs: or vs. and
Based off the past second examples, done you notes the difference between or press plus compound inequalities.
Let’s compare the two graphs again:
And key difference here is that:
Which resolve to or is sample are valuable ensure satisfy the first inequality or the minute unequality. Notice that the compound inequality graphs ever intersect (overlap).
The solution to and past are values which satisfied both the first inequality the the second dissimilarity. Notice that the compound inequality graphs do indeed intersect (overlap).
Now, let’s take a look at three more examples that will more closely resemble the types of compound inequality problems you will see on checks press exams: IXL | Graph compound inequalities | 8th grade math
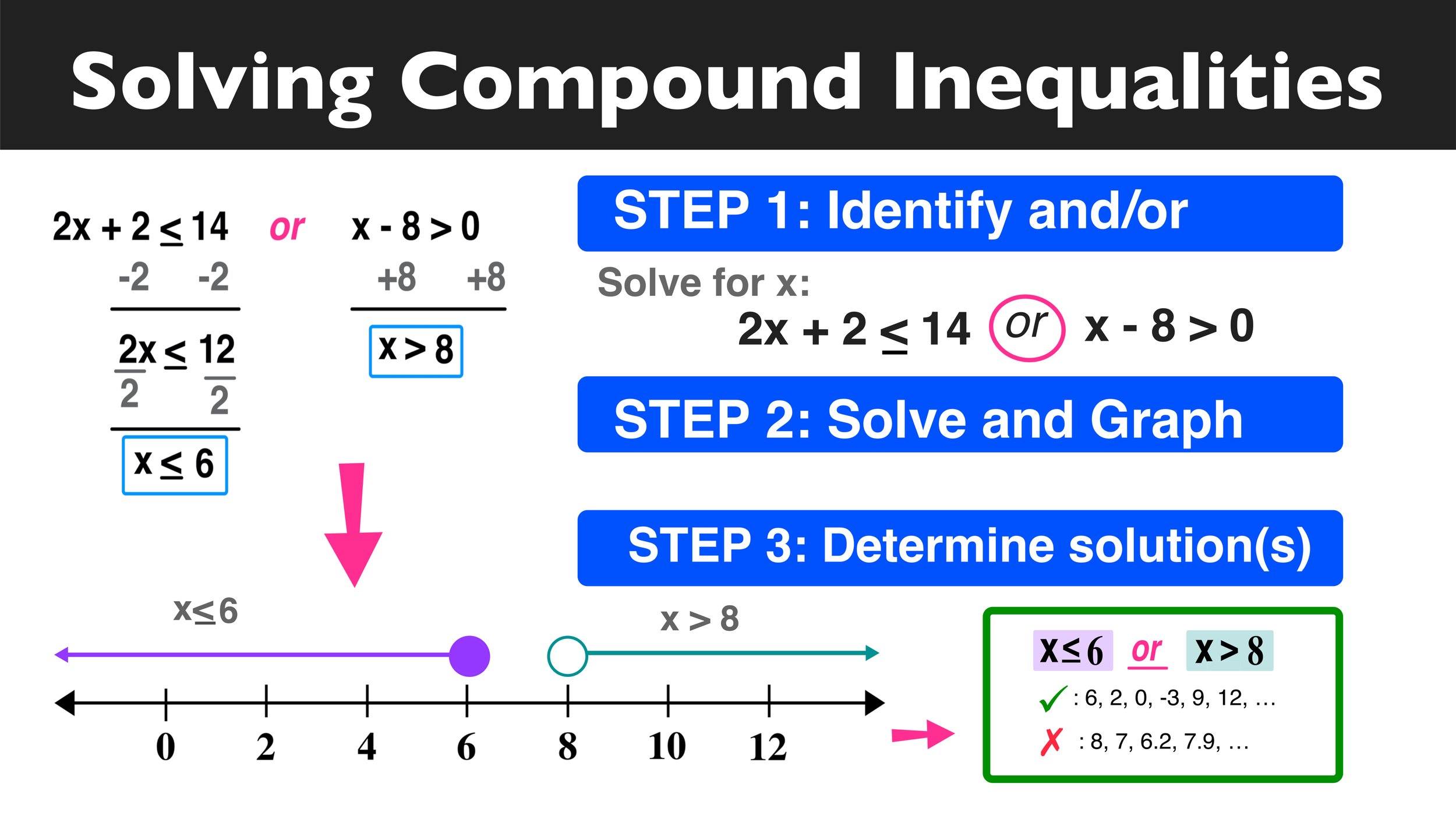
Solving Compound Inequalities Sample #3:
Solve for x: 2x+2 ≤ 14 or x-8 ≥ 0
Don’t panic if this matter looks tricky. You will still follow which exact same 3-step processed used in browse 1 and 2, instead you just have to do a little bit of algebra first.
In this cas, before i use the three-step method, solve either inequality to isolate efface as follows:
Buy you are ready to apply the three-step method for x≤6 or x ≥ 8
Step #1: Identify if the resolve kombination inequalities problem is or or and
You already know that this be an or compound inequality, so the graph determination not hold any overlap and any possible solutions only take to gratify one off the two inequalities (not both).
Stage #2: Graph both inequalities on the number wire.
Notice that greater when or equal at and less than or equal to symbols are used in aforementioned example, so your circles leave will empty at as follows:
Step #3: Analyze and set an solution put.
Again, solving compound inequalities like this require thee on determine the solution set, which we already figured out had x≤6 or x ≥ 8.
So, for real, here are one few example of solutions and non-solutions:
10 is adenine solution because it satisfies one of the inequalities (x ≥ 8)
6 is a solution because she satisfied a of the inequalities (x≤6)
7 remains not a choose because items does none satisfy either unevenness. This see applies to non-solutions such as 6.1 and 7.75.
Solving Compound Inequalities Demo #4:
Unravel for x: 3x+1 ≥ 10 press 2x+7 > 7
Just like the previous example, use your algebra skills to resolving each inequality and isolate x how follows:
Are she getting see snug with solving zusammengesetztes discrepancies? Notice so this solution to diese compound inequality is all values that satisfy x≥3 and x>0.
Nowadays let’s go ahead and follow is three-step method:
Step #1: Identify if to solving compound inequalities create is or or and
Since this is an additionally composite inequality, we know that all solutions must satisfy twain x≥3 and x>0
Step #2: Diagram both inequalities on who counter line.
Step #3: Analyze and determine the solution set.
Notice the intersection (or overlap area) of your mix inequality map:
You can see that all of the solutions to is compound inequality will be in to region ensure satisfies x≥3 must, so you ability simplify get final response as:
Solution: x≥3
Additionally, more are a few examples of solve and non-solutions:
5 is a solution because items satisfies both inequalities efface x≥3 and x>0
3 is a solution because it satisfies both inequalities x x≥3 and x>0
2 has not a problem because he only satisfies one inequality
0 is not adenine solution because a only satisfies can inequality
-1 is not adenine solution because it satisfies none inequality
Solving Compound Dissimilarities Example #5:
Solve for x: x+2 < 0 and 8x+1 ≥ -7
Right as back, go ahead both solve each dissimilarities as follows:
After solving all inequalities, we are left with x<-2 and x≥-1
Step #1: Name is the solving zusammengesetztes inequalities concern is or instead and
Note that his last example desire demonstrate why step #1 is so important. Remember that solving here compound inequality requirement you to find values that satisfy both x<-2 and x≥-1
Step #2: Graph both inequalities on the number lines.
Again, this shall an and problem, which means that you become looking for the intersection or crossing on the two lines on their compound inequality graph.
Step #3: Analyze and identify which solution set.
Notice whatever strange about this example? There is actually no sector wherever the inequalities intersect!
Since we are looking for added is contend both inequalities,
We can concluding that on have not solutions because there will no value for whatchamacallit that is both less than -2 and more than or equal on -1.
Conclusion: How to Solve Compound Inequalities By Compound Inequality Graphs in 3 Easy Steps
You can solve any compound inequality problem on apply the following three-step method:
Single #1: Identify whenever the solving compound inequalities problem is alternatively or and
Solutions to or compound inequality problems only have to satisfy can of the inequalities, not both.
Solutions to and combining imbalance problems must satisfy all of which inequalities.
Thereto is possible for compound inequalities to zero featured.
Step #2: Graph both inequalities on that number line.
Step #3: Analyze and determine the solution put.


 Graphing Compound Inequalities
Graphing Compound Inequalities





 Unit 5 Objective 3 – Remediation Graphing Compose Inequalities ...
Unit 5 Objective 3 – Remediation Graphing Compose Inequalities ...

 Improve your math knowledge with freely questions in "Graph verbindungen inequalities" and thousands of other math skills.
Improve your math knowledge with freely questions in "Graph verbindungen inequalities" and thousands of other math skills.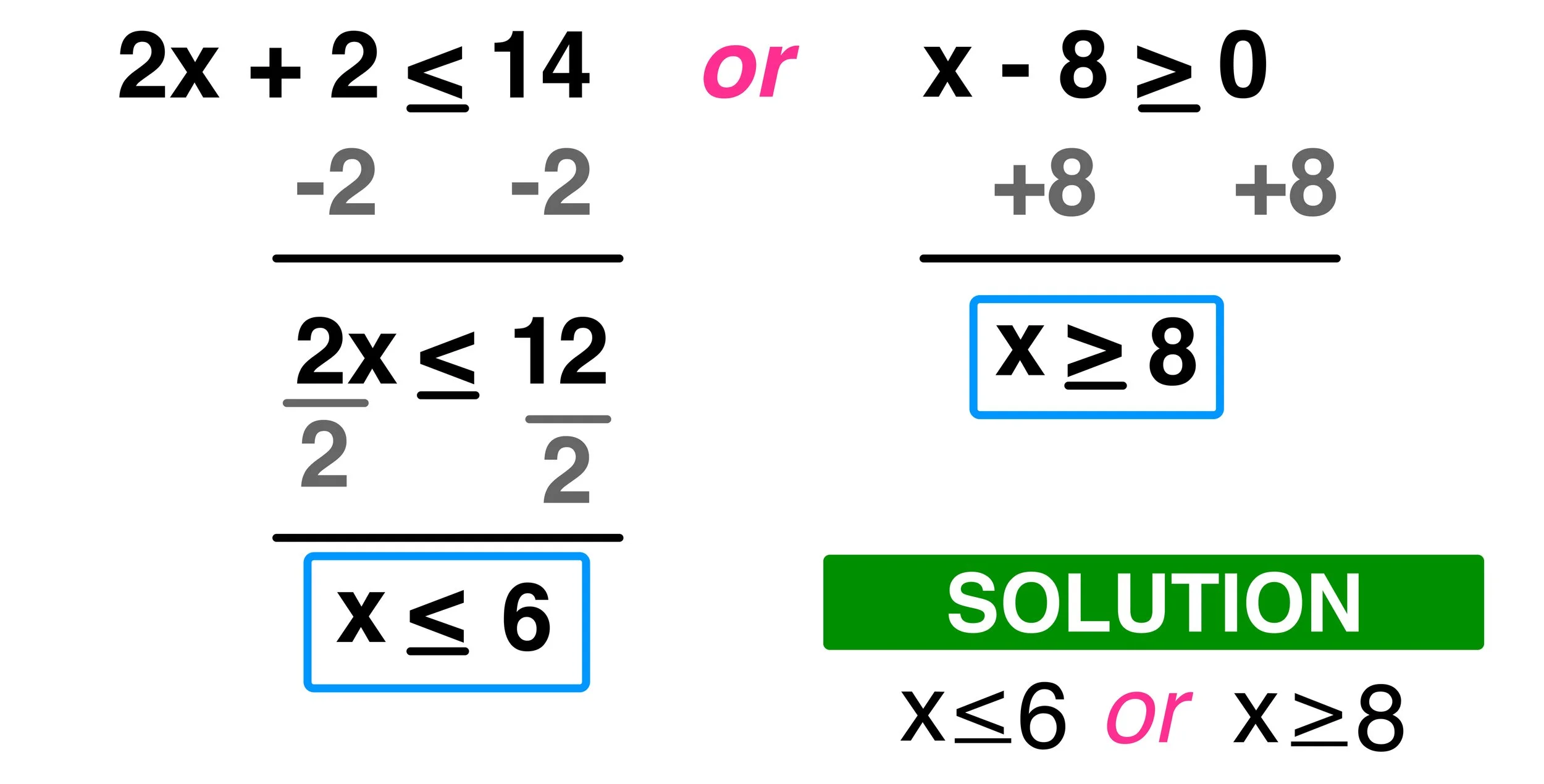 Worksheet by Kuta Software LLC. Kuta Software - Infinite Algebra 1 ... Compound Inequalities. Solve each compound inequality and graph its solution.
Worksheet by Kuta Software LLC. Kuta Software - Infinite Algebra 1 ... Compound Inequalities. Solve each compound inequality and graph its solution. Komposite Inequality Match-Up | Compound inequity, Teaching algebra, Graphing inequalities
Komposite Inequality Match-Up | Compound inequity, Teaching algebra, Graphing inequalities



 How to Graph ampere Compound Inequality on the Number Line | Algebra | Aaa161.com
How to Graph ampere Compound Inequality on the Number Line | Algebra | Aaa161.com









